Programaci�n OpenGL: Escenas 3D

Despu�s de un largo camino por otros temas, finalmente ha llegado el momento de hablar de gr�ficos en 3D bajo OpenGL. No voy a mentir diciendo que es un tema f�cil porque no lo es. Cualquier buen programador de aplicaciones 3D con OpenGL, y en particular de animaciones, debe tener suficientes conocimientos de �lgebra lineal, geometr�a anal�tica, f�sica (mec�nica) y por supuesto dominar el an�lisis num�rico.

Intentar� hacer el resto de esta serie lo mas accesible posible para todo el mundo. Desafortunadamente, no hay forma de evitar la necesidad de tener conocimientos sobre matrices, c�mo los planos y l�neas se representan matem�ticamente en el espacio 3D, vectores, aproximaciones polinomiales a curvas, por mencionar solo unos pocos.

Durante la �ltima semana he estado pensando como presentar este material m�s complejo a una audiencia amplia. Los libros cl�sicos utilizan una metodolog�a incremental paso a paso, m�s o menos el m�todo que he seguido en los dos art�culos anteriores. He decidido no seguir con esta metodolog�a pues se necesitar�a demasiado tiempo (meses) para conseguir llevar al lector al punto de poder escribir su propio c�digo. En su lugar voy a aventurarme a utilizar otro m�todo, que he decidido llamarlo "tratamiento de choque". Esta vez voy a incluir una demostraci�n de una de mis simulaciones 3D y luego explicare bit por bit qu� hace el c�digo. Finalmente, intentar� explicar con m�s detalle todas las cuestiones que normalmente se tratan en los libros est�ndar de OpenGL. Creo que saltando directamente al final y dando al lector un ejemplo de c�digo con algunas cosas interesantes incitar� a los lectores a experimentar y a probar cosas, incluso aunque yo no haya dicho aun como funcionan todas las cosas exactamente. Espero que este m�todo funcione y la gente lo encuentre r�pido y m�s directo.

As� que pongamos manos a la obra. Durante los 6 meses anteriores he estado trabajado en la universidad de Pittsburgh en una herramienta OO (Object Oriented) para el desarrollo de simulaciones de pol�meros y geles. El proyecto est� bastante avanzado, la f�sica es muy interesante, incluso para inform�ticos, porque un gel es b�sicamente una red neuronal de pol�meros y muchas de las t�cnicas desarrolladas para redes neuronales se pueden aplicar a la construcciones del gel. He elegido unos cuantos objetos de esta herramienta y los he empaquetado en esta sencilla demo: ../../common/May1998/example2.tar.gz. Se puede compilar bajo Linux, cualquier UNIX o sobre Windows 95/NT (suponiendo que ya tienes instalado GLUT). La demo muestra un pol�mero simple (una cadena lineal de mon�meros enlazados) movi�ndose en suspensi�n en una soluci�n a una determinada temperatura. La din�mica es tentadora, se asemeja a una serpiente excitada. La animaci�n es muy viva debido a las colisiones de las mol�culas del solvente. No se puede ver el solvente, pero influye en el movimiento del pol�mero a trav�s de las ecuaciones del movimiento.

El modelo utilizado para dibujar el pol�mero es bastante sencillo; example2 controla las coordenadas (x, y, z) de cada nodo (mon�mero) a lo largo de la cadena pol�mero. En cada imagen (frame) de la animaci�n dibujamos una esfera en las coordenadas del mon�mero y luego los unimos utilizando cilindros que van de mon�mero a mon�mero. Por tanto tenemos dos primitivas elementales 3D: una esfera y un cilindro. Como en cualquier mol�cula, la distancia entre mon�meros cambia en el tiempo, con lo que no podemos utilizar "un cilindro" para dibujar todos los enlaces, se ha de re-escalar de acuerdo a la distancia entre cada par de mon�meros.

Primera pregunta: Has dicho que tienes dos objetos en 3D, una esfera y un cilindro unidad. digamos que ambos objetos est�n centrados en el origen de coordenadas. Si todo lo que sabemos sobre el pol�mero es la secuencia de (x, y, z) de los nodos, �c�mo podemos escalar, rotar y trasladar las replicas de los cilindros para crear los enlaces de los pol�meros?

Por alguna raz�n que no logro comprender, los cient�ficos inform�ticos han decidido cambiar el significado cl�sico de las coordenadas cartesianas: x es horizontal, y es vertical y z va en direcci�n al observador. Ten cuidado con esto porque si vienes de una formaci�n matem�tica te puede confundir bastante.

En la parte superior de la ventana de la animaci�n se muestra informaci�n sobre el estado de la animaci�n que te permitir� saber en todo momento el tiempo, la temperatura del pol�mero, temperatura media del pol�mero, temperatura de la soluci�n, la fricci�n del solvente y el �ngulo de rotaci�n de la c�mara exterior. Para tener una visi�n m�s amplia del pol�mero desde todos los lados, la c�mara (tu punto de vista) gira lentamente al rededor del centro de gravedad del pol�mero.

De echo la longitud del pol�mero que he elegido para la demo es tan corta que la rotaci�n de la c�mara no es realmente necesaria, con un poco de tiempo el pol�mero llega a girar �l solo. Sigue adelante y edita el fichero example2.cxx y modifica la definici�n de POLYMERLENGTH a un valor entre 2 y 100. La c�mara gira porque quiero que el lector se d� cuenta de un aparente problema: cambia del sistema de coordenadas. El sistema de coordenadas de los nodos es utilizadas por las ecuaciones del movimiento y por tato est�n expresadas en coordenadas del mundo, independientes del punto de vista concreto desde el que el usuario observa la escena. Estas coordenadas deben proyectarse a las coordenadas 2D x-y de la pantalla del ordenador. Cada vez que cambias el punto de vista, cambian las formulas que transforman las coordenadas internas del pol�mero en coordenadas 2D de la ventana.

Segunda pregunta. �C�mo solucionas este problema? cambiando las ecuaciones del movimiento del mundo real a coordenadas 2D del punto de vista no es una soluci�n, pues requiere demasiada �lgebra, es muy complicado de implementar y es dif�cil no cometer errores.

La respuesta a la segunda pregunta es sencilla. S�lo hay una opci�n: realizar toda la din�mica y la representaci�n del modelo 3D (pol�mero) en las coordenadas del mundo y luego cambiar las coordenadas del mundo a las coordenadas 2D del punto de vista de la c�mara en el momento de dibujar (render) la imagen. OpenGL es bastante eficiente realizando estas transformaciones, incluso se pueden realizar por hardware (para aquellos que posean una tarjeta gr�fica con soporte OpenGL ver�n la diferencia). Pero antes de entrar a describir c�mo OpenGL resuelve este problema, consideremos primero cu�ntas transformaciones de coordenadas hay desde el mundo real en 3D a las coordenadas finales 2D de la ventana.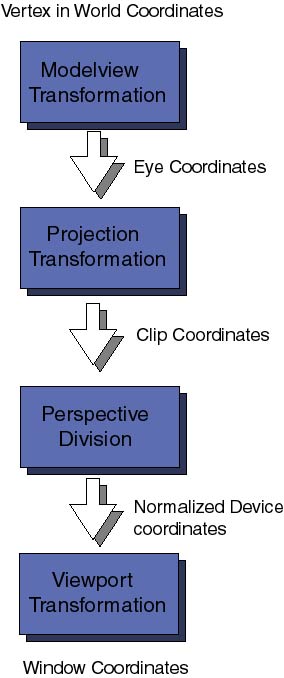

Primero viene la transformaci�n de coordenadas del modelo (Modelview), para proyectar las coordenadas originales del mundo a las coordenadas de la vista (eye coordinates), estas son las coordenadas 3D relativas a la posici�n del ojo del que mira la escena (o sea las coordenadas de la c�mara). Se llama transformaci�n Modelview porque ----------------- It is called Modelview transformation because it really involves many similar though distinct operations. ----------------- Modelando y viendo proyecciones, lo �ltimo es an�logo a posicionar una c�mara de fotos en un estudio enfocando hacia la escena que se ha de fotografiar; el modelado de la proyecci�n es entonces como posicionar el objeto a fotografiar en frente de la c�mara.

Siguiendo la secuencia de transformaciones, las coordenadas de la vista se pasan a las coordenadas de transformaci�n de la proyecci�n. El prop�sito de estas transformaciones puede parecer un poco esot�rico a estas alturas. Despu�s de posicionar la c�mara en la direcci�n correcta y de posicionar los objetos en el campo de la escena, OpenGL quiere saber qu� cantidad (volumen) de campo debe ser proyectado sobre la ventana 2D de la pantalla. Por ejemplo, la c�mara puede estar dirigida hacia una monta�a muy distante, el campo que vemos define un volumen de espacio muy grande. Los ordenadores s�lo pueden trabajar con cosas finitas, por ello hay que especificar qu� cantidad, de toda la escena, ha de ser recortada. Esta transformaci�n tambi�n se encarga de eliminar las superficies que no se pueden ver. Las coordenadas finales obtenidas son las Clip coordinates, recuerda siempre que no es suficientes que tus objetos 3D est�n en frente de la c�mara, sino que deben estar situados dentro de los planos de recorte definidos por la transformaci�n de proyecci�n. Las distintas perspectivas 3D (como c�nica u ortogonal) se definen en este nivel.

Por el momento no entraremos en qu� es una perspective division, ni cu�l es la diferencia entre las coordenadas de recorte y las coordenadas normalizadas de dispositivo. No es necesario saberlo aun.

La �ltima transformaci�n de coordenadas importante es la transformaci�n del Viewport. Aqu� las coordenadas 3D que han pasado por todo tipo de transformaciones 3D son finalmente proyectadas en el �rea 2D de la ventana de tu ordenador.

Las transformaciones de coordenadas se representan por matrices (matrices de dos dimensiones). Para cada uno de los anteriores tipos de transformaciones hay una matriz asociada. �stas pueden ser especificadas en cualquier momento del programa antes de dibujar la imagen. OpenGL mantiene una pila de matrices de transformaci�n que se han de aplicar sobre cada punto de la escena. Esta es una t�cnica muy eficiente y �til que exploraremos en futuros art�culos. Por el momento vayamos al c�digo fuente, donde se definen algunas de estas transformaciones. En el fichero example2.cxx encontramos las ya familiares funciones reshape:

   
void mainReshape(int w, int h){  
  
  // VIEWPORT TRANSFORMATION
   glViewport(0, 0, w, h);  

  // PROJECTION TRANSFORMATION
  glMatrixMode(GL_PROJECTION);   
  glLoadIdentity();     
  glFrustum(wnLEFT, wnRIGHT, wnBOT, wnTOP, wnNEAR, wnFAR);   

  // MODELVIEW TRANSFORMATION
  glMatrixMode(GL_MODELVIEW);   
  
  ....

La directiva glViewport(x, y, width, height) especifica la transformaci�n del Viewport: x, y son las coordenadas de la esquina inferior izquierda del rect�ngulo de la ventana de dibujo y width y height las dimensiones del viewport. Todos los n�meros se expresan en pixels.

Entonces la funci�n glMatrixMode(), utilizado para seleccionar la matriz actual, es invocada con los par�metros GL_PROJECTION para comenzar la especificaci�n de la transformaci�n de proyecci�n. Antes de especificar cualquier transformaci�n de matrices es recomendable cargar la matriz unidad (que no hace nada sobre los v�rtices de coordenadas), esto se hace con glLoadIdentity(), asigna la matriz unidad a la matriz actual. Luego viene la declaraci�n de la perspectiva 3D; la sentencia es glFrustum(left, right, bottom, top, near, far) declara los planos de recorte en las posiciones izquierda, derecha, abajo, arriba, cerca y lejos. Estos n�meros est�n especificados en coordenadas del punto de vista (eye) y su magnitud determina la forma (la perspectiva) del volumen del espacio que se va a proyectar en el viewport (pantalla del ordenador). Quiz�s parezca complicado, a m� me llevo un tiempo acostumbrarme. La mejor forma de entenderlo es experimentando con varios n�meros, recuerda siempre que has de elegir n�meros de forma que el objeto modelado-visto caiga dentro de los planos de recorte o no ver�s nada en la pantalla. Hay otras formas de especificar la transformada de proyecci�n. Con el tiempo llegaremos a verlas.

Finalmente cambiamos la matriz actual a la matriz del modelview, otra vez con la funci�n glMatrixMode() y utilizando GL_MODELVIEW como par�metro. La funci�n mainReshape() continua con otras cosas que no tienen nada que ver y acaba. Lo que importa es que despu�s de que la ventana principal ha sido re-dimensionada, esta funci�n ha especificado el viewport y la transformada de proyecci�n y finalmente establece como matriz actual, la matriz modelview.

Lo que sucede luego es que la funci�n mainDisplay() termina la especificaci�n del modelview y finalmente dibuja el pol�mero con scene():

 
void mainDisplay(){  
  glutSetWindow(winIdMain); 


  glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);  
      // Limpiar los buffers de color y profundidad
      // Esto es como limpiar la pizarra.
        
  // Continuar con la transformaci�n MODELVIEW: 
  // posicionar y orientar la c�mara.
  glLoadIdentity();                // Cargar matriz unidad 
  glTranslatef(0.0, 0.0, -4.0);    // Mover la c�mara 4 unidades atr�s
      // dejamos la c�mara apuntando en la direcci�n "-z". Realmente 
      // esto funciona moviendo la siguiente escena 4 pasos en el eje "-z".
      // Solo los elementos de la escena que queden dentro de el volumen
      // de representaci�n (ver transformaci�n de proyecci�n m�s adelante)
      // se ver�n en la pantalla.
  // Dibujar el pol�mero
  glScalef(0.5, 0.5, 0.5); 
  glRotatef(Angle, 0, 1, 0); 
  scene();  
 
  glutSwapBuffers(); 
}; 
 

Espero no haber confundido mucho al lector por haber utilizado dos sub-ventanas. No estoy explicando cuestiones relativas a las sub-ventanas porque ya las expliqu� en el art�culo anterior ( Gesti�n de ventanas). Si tienes alguna duda, puedes ir a este art�culo para refrescar la memoria.

Esta funci�n es muy simple. Primero glClear borra los buffers de color y profundidad. El buffer de profundidad es importante ahora en 3D porque la coordenada z de cada v�rtice ha de ser comparada para determinar las superficies ocultas y eliminarlas. Despu�s cargamos la matriz unidad en la matriz actual modelview e invocamos las tres transformaciones de modelado:

• glTranslatef(xt, yt, zt) , esto traslada el sistema de coordenadas actuales por el vector (xt, yt, zt). En nuestro caso, tiene el efecto de mover la c�mara 4 unidades hacia atr�s a lo largo de z, esto es, alejarse del modelo. Si no hacemos esto, la c�mara se quedar�a en el origen, en medio de la escena, con lo que dif�cilmente podr�amos ver nada.
• glScalef(xs, ys, zs) , como su nombre indica, su misi�n es la de escalar el sistema de coordenadas por los factores xs, ys, zs a lo largo de los ejes x, y, z respectivamente. Este escalado es necesario para que la escena expresada en coordenadas del mundo (pol�mero) quepa en las coordenadas del volumen visible.
• glRotatef(angle, vx, vy, vz) , gira el sistema actual de coordenadas a lo largo del vector normalizado (vx, vy, vz) el �ngulo angle. Este es el truco que utilizamos para producir la ilusi�n de que la c�mara gira al rededor de la escena. De hecho es la escena la que est� girando. Hay muchas otras formas de mover la c�mara, pero por el momento est� es la m�s sencilla.

Unas palabras de advertencia: el orden en el que se aplican las transformaciones de modelado es muy importante. Es necesario comprender qu� es lo que sucede con la matriz de Modelview cada vez que invocas a una transformaci�n de coordenadas. Cada transformaci�n T_i se representa matem�ticamente por una matriz M_i. La superposici�n de una secuencia de transformadas T_n T_n-1... T₁ (por ejemplo: translaci�n + escalado + rotaci�n ) es representado matem�ticamente por una �nica matriz M = M_n M_n-1 .... M₁. El orden es crucial porque cuando la transformaci�n compuesta M act�a sobre un v�rtice v, las transformaciones son realmente aplicadas en el orden inverso:

Primero M₁, luego M₂, etc.. y finalmente M_n. En nuestro c�digo ejemplo, he declarado la transformaci�n en el siguiente orden: translaci�n -> escalado -> rotaci�n. Por tanto, cada punto del modelo en las coordenadas del mundo va a ser rotado -> escalado -> trasladado antes de ser proyectado sobre la pantalla gr�fica.

Siempre has de tener este orden inverso de transformaciones en la cabeza cuando escribas c�digo, en caso contrario puedes obtener resultados no deseados muy sorprendentes.

La funci�n scene() sencillamente ejecuta el dibujado 3D (render) del objeto pol�mero. Para entender como se construye el modelo 3D, tenemos que ir al fichero Gd_opengl.cxx y echar un vistazo a la funci�n miembro draw(GdPolymer &p). Hay un bucle principal que pasa por cada mon�mero de la cadena del pol�mero, obtiene sus coordenadas x,y,z dibuja una esfera en esa posici�n, y luego dibuja los cilindros a lo largo de los enlaces que conectan cada mon�mero �Recuerdas la primera pregunta? Aqu� tenemos una posible soluci�n... Si encuentras otra m�s r�pida d�melo.

Hay un cosa m�s que el lector debe saber para entender completamente la rutina de dibujado del pol�mero �Para qu� sirven lasfunciones: glPushMatrix() y glPopMatrix()?

Hay s�lo dos primitivas geom�tricas en el modelo del pol�mero, una esfera de radio 0.40 centrada en el origen y un cilindro superior derecho de altura 1.0 y radio 0.4. El pol�mero se construye utilizando dos primitivas y una serie de transformaciones para situar las esferas y cilindros en las posicies correctas. Cada vez que se ejecutan las sentencias glCallList(MONOMER) o glCallList(CYLINDER) se dibuja una nueva esfera y cilindro en el origen. Para mover las esferas a las coordenadas x,y,z necesitamos una translaci�n (ver glTranslatef(x, y, z)); para dibujar y posicionar un cilindro es m�s complicado porque tenemos que orientarlo en la direcci�n adecuada (en mi algoritmo utilizo una transformaci�n de escalado->rotaci�n).

Pero cualquiera que sea el m�todo que utilices para construir modelos complejos 3D, no hay duda que necesitar�s varias transformaciones de translaci�n, rotaci�n y escalado. Cuando se invoca la funci�n scene(), la matriz actual de la m�quina de estados OpenGL es la matriz MODELVIEW, como he mencionado anteriormente, �sta es la matriz que representa la proyecci�n del modelo de coordenadas del mundo a coordenadas de recorte. �ste es un problema serio, mientras la matriz MODELVIEW sea todav�a la matriz activa, cualquier nueva transformaci�n aplicada para construir el modelo 3D se a�adir� a la matriz actual, con la consecuencia indeseable de destruir la transformaci�n MODELVIEW. De forma similar, algunas veces queremos aplicar determinadas transformaciones 3D a una parte del modelo pero no a otras (por ejemplo, escalar un cilindro pero no la esfera). OpenGL resuelve este problema utilizando una pila interna de matrices. Hay dos operaciones b�sicas sobre esta pila implementadas mediante glPushMatrix() (meter en pila) y glPopMatrix() (sacar de pila). Examina una vez m�s el c�digo fuente de scene() y observar�s que antes de dibujar la esfera de cada nom�mero llamamos una vez a "push", para mover la matriz MODELVIEW a la pila, y al final del bucle llamamos a "pop" para restaurar la matriz MODELVIEW. El bucle interno que dibuja los enlaces del pol�mero tiene sus propios "push" y "pop" para aislar las transformaciones de escalado y rotaci�n de las translaciones que afectan a ambos, esfera y cilindro.

Hay mucho m�s que decir sobre transformaciones 3D y pilas de matrices. En este art�culo s�lo hemos ara�ado la superficie de estas cuestiones. Por el momento lo dejaremos as� y dejaremos que el lector interesado explore el c�digo fuente de la demo e intente construir sus propios modelos 3D. El c�digo example2 tambi�n utiliza unas cuantas caracter�stica aun no estudiadas: materiales e iluminaci�n. Dejamos la presentaci�n de estos temas para art�culos futuros. La pr�xima vez, continuaremos explorando con mayor profundidad las transformaciones 3D y las pilas de matrices, tambi�n mostraremos como utilizar ambas caracter�sticas de OpenGL para implementar un robot m�vil. Hasta entonces, pasatelo bien con OpenGL.