OpenGl : Rendu de sc�ne 3D

Apr�s une longue discussion sur d'autre aspect d'OpenGL, voici finalement venu le temps de parler de graphique 3D. Je ne vous mentirais pas en disant que c'est un sujet facile, car ce n'en est pas un. Tous les bon programmeurs d'applications 3D sous OpenGL, et en particulier d'animations, doivent avoir des connaissances en alg�bre lin�aire, g�om�trie analytique, physique (m�canique) et bien sure un peu d'analyse num�rique.

Je vais essayer de rendre le reste de cette s�rie aussi accessible que possible � tous. Malheureusement, on ne peut se passer de connaissances sur les matrices, sur la repr�sentation math�matique des plans et surfaces dans l'espace, sur les vecteurs et l'approximation polynomiale de courbes, pour n'en citer que quelques-uns.

Durant ces derni�res semaines, je me suis longtemps interrog� sur la mani�re de pr�senter cela � l'audience la plus large. Les livres classiques suivent une approche �tape par �tape, plus ou moins ce que j'ai fais dans les premiers articles. J'ai d�cid� ne de plus suivre cette m�thode car elle nous prendrait beaucoup trop de temps (des mois!) pour amener le lecteur au point ou il lui serait possible d'�crire son propre code. Aussi, vais-je m'essayer � une autre m�thode que j'appellerai le "traitement de choc". Ce mois-ci, je vais inclure dans cet article une d�mo de l'une de mes simulations 3D, et ensuite essayer de vous expliquer pas � pas ce qu'il y a dans le code. Eventuellement nous explorerons en d�tail les sujets abord� traditionnellement dans les livres sur OpenGL mais je crois que donner au lecteur un exemple complet, am�nera le lecteur � exp�rimenter et essayer certains choses par lui-m�me malgr� le fait que je n'expliquerai pas ici tous les d�tails. J'esp�re que cette m�thode marchera et sera plus directe.

Fini le B.A.BA! Durant les six derniers mois, j'ai travaill� � l'universit� de Pittsburgh sur une boite � outils logicielle Orient�e Objets pour faciliter le d�veloppement de simulations sur les gels et polym�res. Le projet est maintenant bien avanc�, la physique qui sous-tend tout cela est tr�s int�ressantes m�me pour les informaticiens car un gel peut-�tre vu comme un r�seaux de neurones de polym�res et la plupart des techniques d�velopp�es pour les r�seaux neuronaux s'appliquent � la construction de gel. J'ai pioch� quelques objets de cette biblioth�que et je les ai mis dans un exemple ../../common/May1998/example2.tar.gz Il peut �tre compil� sous Linux, la plupart des UNIX ainsi que sous Windows95/NT si GLUT est install�. La d�mo montre un seul polym�re (une cha�ne de plusieurs monom�res reli�s entre eux) en mouvement lorsqu'il se trouve plong� dans une solution � une temp�rature donn�. La simulation est fascinante, cela ressemble � un serpent que l'on taquinerai! Cette "vie" est due aux collisions avec les mol�cules de solvant. Vous ne verrez pas le solvant car son action est int�gr�e aux �quations de mouvement du polym�re.

Le mod�le utilis� pour simuler le polym�re est assez simple; example2 m�morise les coordonn�es (x, y ,z) de chaque noeud (monom�re) tout au long de la cha�ne du polym�re. A chaque image de l'animation, nous dessinons une sph�re aux coordonn�es d'un monom�re que nous relions ensuite par des cylindres. Le polym�re � donc deux primitives 3D principales: une sph�re et un cylindre. Comme avec toutes les mol�cules, la distance entre monom�res varie au cours du temps, et nous sommes donc oblig� d'utiliser plusieurs cylindres de longueurs diff�rentes.

Question 1: Vous disposez de deux objets 3D, une sph�re et un cylindre vertical de hauteur 1. Les deux objets sont centr�s � l'origine du rep�re de coordonn�es. Tout ce que vous connaissez � propos du polym�re c'est la s�quence des coordonn�es (x, y, z) des noeuds. Comment allez vous appliquer les diff�rentes transformations que sont: le changement d'�chelle, la rotation, la transformation sur les copies de nos primitives pour construire le polym�re?

Pour des raisons qui me sont inconnues, les informaticiens ont d�cid� de ne pas respecter l'ordre commun�ment admis pour les coordonn�es cart�siennes: ici, X est horizontal, y vertical et Z viens vers l'observateur. Rappelez-vous de cela car si vous venez des math�matiques ou des sciences cela vous perdra un peu au d�but.

Il y a une jolie zone d'information au sommet de la fen�tre qui vous indique la date courante, la temp�rature actuelle du polym�re, sa temp�rature moyenne ainsi que la temp�rature de la solution, le coefficient de frottement du solvant et l'angle de rotation de la cam�ra ext�rieure. Afin de donner une vue la plus large du polym�re, la cam�ra (votre point de vue) tourne lentement autour du centre de gravit� du polym�re.

En fait la longueur de polym�re que j'ai choisi pour cette d�mo est si courte que faire tourner la cam�ra n'est pas vraiment n�cessaire car le polym�re tourne de lui m�me. SI vous le voulez, �ditez le fichier example2.cxx et modifiez la d�finition de POLYMERLENGTH entre 2 et 100. La cam�ra tourne car j'ai voulu que le lecteur prenne conscience d'un probl�me: Le changement de syst�me de coordonn�es. Les coordonn�es des noeuds utilis�es par les �quations de mouvements sont d�finis en coordonn�es absolues ( se sont les coordonn�es du "monde") et sont ind�pendante du point de vue de l'observateur. Ces coordonn�es sont projet�es sur les syst�me de coordonn�es 2D de l'�cran. A chaque fois que le point de vue change, les formules n�cessaire � cette projection changent.

Question 2: Comment r�soudriez vous ce probl�me? Transformer les �quations de mouvement de coordonn�es du monde en coordonn�es 2D de l'observateur et hors de questions, cela entra�nerai trop de calculs, serait compliqu� � coder et cela ferai beaucoup d'erreurs.

La r�ponse � la question 2 est simple, il n'y a qu'une solution pour calculer le mouvement, calculer la repr�sentation 3D et r�aliser la transformation vers le dispositif de rendu (NDT: "viewport" en anglais) � chaque image. OpenGL! OpenGL est efficace pour ce genre de choses elles sont m�me parfois r�alis�es par les cartes graphiques (ceux qui en poss�dent verront la diff�rence). Mais avant de voir comment OpenGL r�pond � ce probl�me, regardons combien il y a de transformation entre les coordonn�es "r�elles" du monde 3D et les coordonn�es 2D finales sur l'�cran.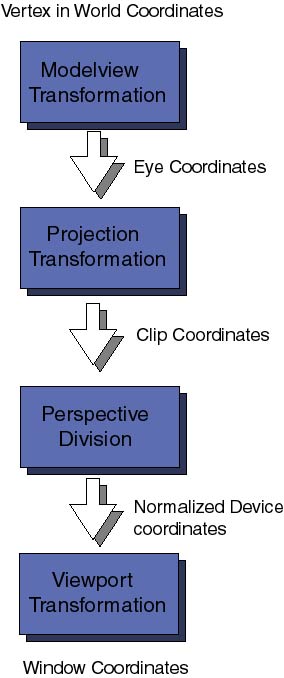

En premier viennent les transformations sur le mod�le (Modelview Transformation sur le sch�ma), elles ont pour but de transformer les coordonn�es absolues du mod�le du monde en coordonn�es "cam�ra". Ce sont donc des coordonn�es tridimensionnelles relatives � l'observateur. On les appelle Modelview car ces transformations bien que diff�rentes se ressemblent fortement : le modelage et la visu; la derni�re est analogue au positionnement d'une cam�ra, la premi�re correspondant au placement des objets dans la sc�ne � photographier.

En continuant le long du tube des diff�rentes transformations, les coordonn�es "cam�ra" sont transmises aux Projections. Le r�le de ces transformations pourront para�tre un peu �sot�rique au premier abord. Apr�s avoir plac� la cam�ra et les objets dans le champs de vision, OpenGL veut savoir quelle proportion de ce champs de vision doit �tre pris en compte. Par exemple, la cam�ra peut-�tre dirig�e vers une montagne lointaine, le champs de vision est alors tr�s large. Les Ordinateurs ne pouvant prendre en compte un nombre finis de choses nous devons d�finir quelle proportion du champs de vision doit �tre coup�e (clip en anglais, le plan de coupe s'appelant clipping plane par exemple. NDT). cette transformation s'occupe �galement d'enlever les faces cach�es � l'observateurs. Les coordonn�es ainsi obtenues sont les coordonn�es de clipping, m�morisez d�s � pr�sent, qu'il ne suffit pas que votre objet soit devant la cam�ra pour �tre vu, il faut �galement qu'il soit � l'int�rieur du volume visible. Les diff�rentes perspectives possibles (conique, orthogonale par exemple) sont d�finies � ce niveau.

Pour le moment nous n'entrerons pas dans la description de la division de perspective ni dans la diff�rence entre les coordonn�es de clipping et les les coordonn�es normalis�es pour un dispositif donn�. Ce n'est pas encore n�cessaire.

La derni�re �tape importante dans les transformations, est projection sur le dispositif de rendu (pour nous l'�cran de l'ordinateur - le viewport en anglais). c'est ici que les coordonn�es 3D sont projet�e sur l'espace 2D de l'�cran.

Les coordonn�es de transformations sont repr�sent�es par des matrices (tableaux bidimensionnels de coefficients). Pour chacune des transformations ci-dessus, il y a une matrice associ�e. Elles peuvent �tre sp�cifi�es � n'importe quel moment dans le programme avant de d�clencher le rendu. OpenGL garde sur une pile, les matrices de transformation devant s'appliquer � chaque points de la sc�ne. C'est une technique efficace et puissante que nous �tudirons plus avant dans de prochains articles. Pour le moment plongeons dans le code source et voyons comment certaines de ces transformations sont d�finies. Dans le programme example2.cxx il ya la d�sormais c�l�bre fonction reshape :

   
void mainReshape(int w, int h){  
  
  // VIEWPORT TRANSFORMATION
   glViewport(0, 0, w, h);  

  // PROJECTION TRANSFORMATION
  glMatrixMode(GL_PROJECTION);   
  glLoadIdentity();     
  glFrustum(wnLEFT, wnRIGHT, wnBOT, wnTOP, wnNEAR, wnFAR);   

  // MODELVIEW TRANSFORMATION
  glMatrixMode(GL_MODELVIEW);   
  
  ....

la directive glViewport(x,y,width,height) sp�cifie le type de projection sur l'�cran. : x, y sont les coordonn�es du coin inf�rieur gauche de la fen�tre de projection et width, heigth sont les dimensions de la zone de rendu. Tous ces nombres sont donn�s en pixels.

Ensuite glMatricMode(), utilis� pour s�lectionner la matrice courante, est appel�e avec le param�tre GL_PROJECTION af in de pouvoir sp�cifier le contenu de la matrice de projection. Avant d'entrer une quelconque des matrices de transformation, il est conseill� de charger la matrice identit� (qui ne r�alise aucune transformation), ce qui est fait par glLoadIdentity() qui remet � z�ro la matrice courante. Ensuite vient la d�claration de la perspective utilis�e; l'ordre glFrustrum(left, rigth, bottom, top, near, far) declare le plan de coupe (clipping plane) � la position left, rigth, bottom, top,near and far. Ces nombres sont donn�s en coordonn�e de vue et leur grandeurs d�termine la forme (donc la perspective) du volume de la sc�ne qui sera projet� sur l'�cran. Peut-�tre cela vous para�t-il un peu compliqu�, j'ai �galement mis un certain temps pour m'y faire. Le mieux pour appr�hender cela est de faire quelques essais avec diff�rents nombres, rappelez vous seulement que quelque soit les nombres choisis les coordonn�es mod�le-vue doivent rester � l'int�rieur du volume de vue sinon rien n'appara�tra � l'�cran. Il y a d'autre moyen de sp�cifier les transformations de projections, nous y viendrons plus tard.

Enfin, nous changeons la matrice courante de mod�le-vue, de nouveau par glMatrixMode() en utilisant le param�tre GL_MODELVIEW. La fonction MainReshape continue ensuite avec d'autre lignes qui n'ont rien � voir avec les transformations et se termine. Ce qui compte ici c'est qu'apr�s un retaillage de la fen�tre principale, cette fonction � sp�cifi� la matrice de projection sur l'�cran, la matrice de transformation et � fait de la matrice mod�le-vue la matrice courante.

La fonction mainDisplay() termine la sp�cification de la matrice mod�le-vue et finalement d�fini le polym�re par la fonction scene() :

 
void mainDisplay(){  
  glutSetWindow(winIdMain); 


  glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);  
      // Clear the color and depth buffers    
      // This is like cleaning up the blackboard    
        
  // CONTINUE MODELVIEW TRANSFORMATION: Set and orient the camera    
  glLoadIdentity();                // Load unity on current matrix
  glTranslatef(0.0, 0.0, -4.0);    // Move the camera 4 steps back    
      // we leave the camera pointing in the -z direction. Actually    
      // this operates by moving the following scene 4 steps in the -z    
      // direction. Only the elements of the scene that fall inside the    
      // viewing volume (see projection transformation later) will appear     
      //on screen.    
      
  // Render polymer  
  glScalef(0.5, 0.5, 0.5); 
  glRotatef(Angle, 0, 1, 0); 
  scene();  
 
  glutSwapBuffers(); 
}; 
 

Cette fonction est assez directe et simple. Tout d'abord glClear() efface le tampon de rendu et d'information de profondeur.. Le tampon contenant ces informations est important car la coordonn�e de profondeur de chaque point doit �tre test� pour savoir s'il est visible ou non et de la si telle ou telle surface doit �tre supprim�e ou gard�e. Ensuite nous chargeons la matrice identit� sur la matrice courante mod�le-vue et appelons 3 transformations :

• glTranslatef(xt, yt, zt) , qui d�place le syst�me de coordonn�es courant de (xt, yt, zt). Dans notre cas cela a pour effet de nous �loigner de 4 unit� du mod�le. Si nous ne faisions pas cela, la cam�ra resterait � l'origine (en plein milieu du mod�le) et nous ne verrions pas grand chose...
• glScalef(xs, ys, zs) , comme son nom l'indique, � pour but de r�aliser un changement d'�chelle de facteurs xs, ys et zs sur les axes x, y and z respectivement. Ce changement d'�chelle est n�cessaire pour faire tenir le polym�re � l'int�rieur du volume de clipping.
• glRotatef(angle, vx, vy, vz) , tourne le syst�me de coordonn�es autour du vecteur normalis� (vx, vy, vz) de "angle" degr�s. C'est ce que nous utilisons pour donner l'illusion d'une cam�ra tournant autour du mod�le alors qu'en fait nous faisons tourner le mod�le. Il y a de nombreuses mani�re de bouger la cam�ra mais pour l'insatnt celle-ci est la plus simple.

Un petit avertissement : L'ordre des transformations est important. Vous devez comprendre ce qui arrive � la matrice mod�le-vue � chaque fois que vous demandez une transformation de coordonn�es. Chaque transformation T_i est repr�sent�e math�matiquement par une matrice M_i. la superposition de s�quence de transformation T_n T_n-1... T₁ (par exemple : translation + homoth�tie + rotation ) est repr�sent� par une seule matrice M = M_n M_n-1 .... M₁. L'ordre est crucial car lorsque une transformation composite M est appliqu� sur un vecteur v les transformations sont en fait appliqu�es dans l'ordre inverse :

D'abord M₁,ensuite M₂, etc.. et finalement M_n. Dans notre exemple, J'ai d�clar� les transformations dans l'ordre translation -> homoth�tie -> rotation, donc chaque point de notre mod�le sera tourn� -> agrandi -> d�plac� avant d'�tre projet� sur l'�cran. Gardez cela pr�sent � l'esprit lorsque vous �crivez du code ou bien vous aurez droit � des r�sultats surprenant.

La fonction scene() se contente de lancer le rendu 3D du polym�re. Pour comprendre comment le mod�le 3D est construit, il faut dans le fichier GD_opengl.cxx regarder la fonction draw(GdPolymer &p). Il y a une boucle principale qui parcoure la liste des monom�res r�cup�re leur coordonn�es (x, y, z), dessine une sph�re � cet endroit, dessine et relie par un cylindre les monom�res adjacents. Vous vous rappelez de la question 1, voil� une r�ponse possible, si vous en connaissez une plus rapide, n'h�sitez pas � nous le dire.

Il y a encore une chose que le lecteur doit savoir pour comprendre int�gralement la routine de rendu du polym�re. A quoi servent ces glPushMatrix() et glPopMatrix() ?

Il n'y a que deux primitives g�om�triques dans le mod�le du polym�re. Une sph�re de rayon 0.40 centr�e � l'origine et un cylindre de hauteur 1 et de rayon 0.40 . Le polym�re est dessin� en utilisant ces deux primitives plus une s�rie de transformations afin de les placer au bon endroit. A chaque appel de glCallList(MONOMER) ou glCallList(CYLINDER), une sph�re ou un cylindre est dessin�e � l'origine. Pour bouger la sph�re aux coordonn�es (x, y, z) nous utilisons une translation (cf. glTranslatef(x,y,z)); pour dessiner et placer le cylindre qui relie deux sph�res, c'est un peu plus complexe car nous devons tout d'abord lui donner la bonne longueur (i.e la distance entre les deux sph�res), puis l'orienter dans la bonne direction(i.e une rotation) - dans mon algorithme j'utilise un changement d'�chelle -> une rotation.

Mais quelque soit la m�thode que vous utilisiez pour dessiner votre mod�le 3D vous aurez besoin de telles transformations. Lorsque la fonction scene() est appel�e la matrice courante de la machine � �tat d'OpenGL est la matrice MODELVIEW, comme nous l'avons pr�c�demment dit, cette matrice repr�sente la projection des coordonn�es du monde dans celle de clipping. Il y a l� un s�rieux probl�me, comme la matrice MODELVIEW est encore la matrice courante, toutes les transformations futures appliqu�es pour dessiner le mod�le seront compos� avec cette matrice et donc d�truira les valeurs de la transformation mod�le-vue. De m�me, nous avons parfois envie de n'appliquer des transformations qu'� une partie du mod�le mais pas aux autres (par exemple : changer l'�chelle du cylindre, mais pas de la sph�re). OpenGL r�sout ce probl�me en utilisant une pile interne pour les matrices. Il y a deux op�rations de base sur cette pile : push (i.e l'empilement) impl�ment� par glPushMatrix() et pop (i.e le d�pilement) impl�ment� par glPopMatrix(). Regardez nue fois encore le code de scene() et notez qu'avant de d�clarer chaque sph�re du monom�re nous appelons l'op�ration d'empilement ce qui met la matrice MODELVIEW sur la pile et en fin de d�claration l'op�ration de d�pilement ce qui restaure la matrice MODELVIEW. De m�me pour les cylindres afin d'isoler les op�rations de mise � l'�chelle et de rotation de l'op�ration de translation qui elle affecte � la fois la sph�re et le cylindre.

Il y aurait encore beaucoup � dire sur les transformations 3D et la pile de matrices. Dans cet article, nous n'avons que soulev� un coin du voile sur ces sujets. Pour le moment nous laisserons le sujet dans l'�tat en laissant le soin au lecteur int�ress� explorer le code source et essayer ses propres mod�les. Le code de example2 utilise un certain nombre de fonctionnalit�s dont nous n'avons pas encore parl� : les mat�riaux et l'�clairage, que nous gardons pour un article futur. Dans le prochain article nous creuserons un peu plus les transformations 3D et la pile de matrice, nous montrerons �galement comment utiliser OpenGL pour animer un robot. d'ici l�, amusez vous avec OpenGL.