OpenGL Programlama: Basit �okgen G�r�nt�le�tirimi

Giri�

Bu yaz�, 2 ve 3 boyutlu grafikler i�in bir end�stri �l��n� (standard�) olan OpenGL hakk�ndaki makale dizisinin ilkidir. (Bak�n�z: OpenGL Nedir?). Okuyucunun, C geli�tirme �al��mataban�na al���k ve GLUT kitapl��� hakk�nda baz� bilgilere sahip oldu�unu kabul ediyoruz (Aksi durumda bu dergideki "GLUT programlama" konusundaki yaz�lar�n izlenmesi gerekir). Linux alt�nda �al���rken, OpenGL konusunda �zg�r kullan�ma a��k e�siz uygulamalar� bulunan Mesa-kitapl���n� kullanman�z� �neririz.Bu anda Mesa i�in donan�m deste�i bile bulunmaktad�r. (Bak�n�z: 3Dfx grafik kart�).

Yeni OpenGl g�d�mlerinin sunumu, en az bizim de yapmaya �abalayaca��m�z kadar, onun i�levselli�ini kullanmaya �al��an bir �rnek ile s�regidecektir. Dizimizin sonunda b�t�n�yle OpenGL ile yaz�lm�� bir oyun �yk�n�m�n� (sim�lasyonu), kaynak d�zg�s�yle (koduyla) birlikte verece�iz.

Ba�lamadan �nce, bir bilim adam� oldu�um i�in, OpenGL deneyimimin b�y�k bir �o�unlu�unun, OpenGL'in ger�el kuvantum ve k�kle�ik (klasik) sistemlerin �yk�n�mlerini (simulasyonlar�n�) yazmak i�in bir ara� oldu�unu s�ylemek isterim. Bu nedenle �rneklerim biraz bu y�ndedir. ;-). Okuyucunun bu �rnekleri eri�ilebilir ya da en az�ndan e�lenceli bulaca��n� umuyorum. E�er farkl� �rnekler g�rmek istiyorsan�z, beni duyumlu k�lman�z (haberdar etmeniz) yeterlidir.

OpenGL, s�kl�kla 3 boyutlu grafiklerle, �zel etkilerle, karma��k �rneklerin ���kla ger�ek modellemesi gibi konularla ilgilidir. Bunun yan�nda 2 boyutlu grafikleri g�r�nt�le�tirmeye (render) yarayan bir makinedir. 3 boyutlu g�r�ngelerin (perspektiflerin) karma��kl���, model g�r�nt�le�tirme, ���k, g�r�nt��eker (kamera) konumu ve bu gibi konular� ��renmeye ba�lamadan �nce 2 boyutta yapmay� ��renebilece�iniz pek �ok �ey olmas� bak�m�ndan bu konu �nemlidir. M�hendislikle ve bilimsel konularla ilgili �ok say�da uygulama 2 boyutta g�r�nt�le�tirilebilir (rendered). Dolay�s�yla, ilk olarak baz� basit 2 boyut canland�r�mlar�n�n (animasyonlar�n�n) nas�l yap�ld���n� ��renmek yerinde olacakt�r.

Noktalar�n �izimi

OpenGL yaln�zca birka� geometrik temel�geye sahiptir: noktalar, do�rular ve �okgenler. Bunlar�n her biri kendilerine ait olan k��eler ile tan�mlan�r. Bir k��e 2 ya da 3 kayarnoktal� say� (floating point number) ile �zyap�land�r�l�r (karakterize edilir), k��enin kartezyen koordinatlar�, 2 boyutta (x,y) ve 3 boyutta (x,y,z)'dir. Kartezyen koordinatlar �ok yayg�n olmakla beraber, bilgisayar grafiklerinde ayr�ca her noktan�n (x,y,z,w) 4 kayarnoktal� say� ile g�sterildi�i benze�ik (homojen) koordinat sistemi de vard�r. 3 boyutun temel �zelliklerini inceledikten sonra bunlara geri d�nece�iz.

OpenGL'de t�m geometrik nesneler bir s�ral� k��eler k�mesi olarak tan�mland���ndan, bir k��enin belirtimi i�in bir yordam demeti bulunmaktad�r.; Kullan�m� ��yledir:

void glVertex{234}{sifd}[v](TYPE coords); 

Haydi, bu kullan�ma al��kanl�k edinelim.{} imleri aras�ndaki s�zc�k yordam�n ad�n� g�stermektedir.; Yordamlar short, long, float ya da double t�rde 2, 3 ya da 4 parametre alabilirler. Se�imeba�l� olarak bu parametreler vektor formda verilebilir, biz v-tip yordamlar� kullanaca��z. ��te baz� �rnekler:

void glVertex2s(1, 3);
void glVertex2i(23L, 43L);
void glVertex3f(1.0F, 1.0F, 5.87220972F);

float vector[3];
void glVertex3fv(vector);

Basitle�tirmek i�in bu yordamlar�n t�m� glVertex* olarak tan�mlan�rlar.

OpenGL, herhangi bir k��e dizisini i�eri�ine g�re yorumlar. Bu i�eri�in belirtimi glBegin(GLenum mode) ve glEnd(), yordam ikilisiyle yap�lmaktad�r. Bu iki yordam aras�nda �al��t�r�lan herhangi bir glVertex* deyimi kip (mod) de�erine g�re yorumlan�r. �rne�in:

glBegin(GL_POINTS);
glVertex2f(0.0, 0.0);
glVertex2f(1.0, 0.0);
glVertex2f(0.0, 1.0);
glVertex2f(1.0, 1.0);
glVertex2f(0.5, 0.5);
glEnd();

2 boyutta 5 nokta �izer. GL_POINTS, OpenGL ba�l�k dosyas�nda <GL/gl.h>. tan�mlanm�� etiketlerden birisidir. Daha pek �ok uygun kip (mod) vard�r ancak, bunlardan, gerekti�inde, s�zedilecektir. 

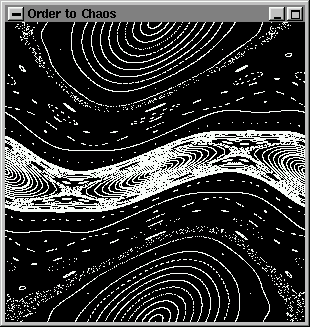
Her nokta, OpenGL'in renk arabelle�i (buffer) ile ili�kili durum de�i�kenlerinde o anda saklanan renklerle �izilir. Ge�erli rengi de�i�tirmek i�in glColor* yordam demetini kullan�n. Renkleri se�mek ve uygulamak hakk�nda s�ylenecek �ok �ey vard�r (Di�er bir yaz� yaln�zca bu konuda olacakt�r). 0.0'dan 1.0'a kadar 3 tane kayarnoktal� de�er kullanarak RGB (K�rm�z� - Ye�il - Mavi) renkleri tan�mlayabiliriz.
glColor3f(1.0, 1.0, 1.0); /* Beyaz */ 
glColor3f(1.0, 0.0, 0.0); /* K�rm�z�*/ 
glColor3f(1.0, 1.0, 0.0); /* Magenta*/ 
etc... 

Buraya kadar anlat�lanlar ilk iki �rnek d�zg�m�z� (kodumuzu) yazmak i�in yeterli malzemeyi olu�turmu� bulunmaktad�r. �lk �rnek, karga�asal (kaotik) d�n���mde (�l��nl� d�n���m, standart d�n���m) bir�ok y�r�nge �izen basit bir OpenGL program�d�r. Okuyucunun d�n���mler ve �zellikle �l��nl� (standart) d�n���mler konusunda bilgili olmamas� sorun de�ildir. Basit�e s�ylemek gerekirse, bir d�n���m�n bir noktay� al�p iyi tan�ml� bir ba��nt� arac�l���yla yeni bir nokta �retir:

y_n+1 = y_n + K sin(x_n)
x_n+1 = x_n + y_n+1

�l��nl� (standart) d�n���m durumunda y�kl� bir par�ac���n, par�ac�k h�zland�r�c�n�n simitinde h�zland�r�c�n�n d�zlemini keserek yapt��� devinimde b�rakt��� izi betimleyen bir model s�zkonusu olur. Bunun ve di�er d�n���mlerin incelenmesi, �emberselh�zland�r�c� i�ine kapat�lm�� bir y�kl� par�ac���n deviniminin kararl�l���n�n anla��lmas� a��s�nda fizikte �ok �nemlidir. �l��nl� (standart) d�n���m, parametresinin baz� de�erleri i�in K'n�n a��k�a karga�asal (kaotik) ve tutuklu devinimin (trapped motion) bir kar���m�n� g�stermesinden dolay� �ok donuktur??????. Sonu� olarak, fizik ile ger�ekten ilgilenilmese de bir �ok g�zel grafik d�zg� (kod) geli�tirmek isteyenler �l��nl� (standart) d�n���mlere yeterince dikkat etmelidirler. Doku, ate� parlamas�, a�a�lar, karapar�alar� gibi �eyleri �retmekte kullan�lan pek �ok algoritma fractal d�n���mlere dayand�r�lmaktad�r. 

../../common/January1998/../../common/January1998/example1.c'nin kaynak d�zg�s� (kodu):

    
#include <GL/glut.h>
#include <math.h>  

const  double pi2 = 6.28318530718;

void NonlinearMap(double *x, double *y){
    static double K = 1.04295;
    *y += K * sin(*x);
    *x += *y;
    *x = fmod(*x, pi2);
    if (*x < 0.0) *x += pi2;
};

void winInit(){
    /* Set system of coordinates */
    gluOrtho2D(0.0, pi2, 0.0, pi2);
};

void display(void){
    const int    NumberSteps = 1000;
    const int    NumberOrbits = 100;
    const double Delta_x = pi2/(NumberOrbits-1);
    int step, orbit;

    glColor3f(0.0, 0.0, 0.0);
    glClear(GL_COLOR_BUFFER_BIT);
    glColor3f(1.0, 1.0, 1.0);

    for (orbit = 0; orbit < NumberOrbits; orbit++){
      double x, y;
      y = 3.1415;
      x = Delta_x * orbit;

      glBegin(GL_POINTS);
      for (step = 0; step < NumberSteps; step++){
        NonlinearMap(&x, &y);
        glVertex2f(x, y);
      };
    
      glEnd();
    };

    for (orbit = 0; orbit < NumberOrbits; orbit++){
      double x, y;
      x = 3.1415;
        y = Delta_x * orbit;

        glBegin(GL_POINTS);
        for (step = 0; step < NumberSteps; step++){
          NonlinearMap(&x, &y);
          glVertex2f(x, y);
        };
        glEnd();

     };
};

int main(int argc, char **argv) {
  glutInit(&argc, argv);  
  glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA);  
  glutInitWindowPosition(5,5);  
  glutInitWindowSize(300,300);  
  glutCreateWindow("Standard Map");  
  
  winInit();
  glutDisplayFunc(display);  
  glutMainLoop();  
  
  return 0;  
}  
  

Pencere ba�lat�m yordam�nda yani winInit() 'da OpenGL elayg�t tak�m�ndan gelen yaln�zca tek bir deyim bulundu�una dikkat �ekmek gerekir:gluOrtho2D(). Bu yordam 2 boyutlu dik sistemin koordinatlar�n� g�sterir. Fonksiyona ge�en parametreler "minimum x, maksimum x, minimum y, maksimum y" dir.
�ekIi �izimin ilk an�ndan ba�layarak g�rebilme �ans�n�z olmas� i�in tek bir ekran modu ve �ok say�da nokta se�tim. Bu b�y�k ve zaman gereksinimi y�ksek olan g�r�nt�ler durumundaki tek kip i�in al���lan bir tav�rd�r, nesneler OpenGL yordamlar�yla ya�amage�irildik�e ekran�n�zda g�r�n�urler. 

../../common/January1998/example1'i �al��t�rd�ktan sonra �u �ekli g�receksiniz:

�imdi ikinci programa ge�elim, ../../common/January1998/../../common/January1998/example2.c:

    
#include <GL/glut.h> 
#include <math.h>

const  double  pi2 = 6.28318530718; 
const  double  K_max = 3.5;
const  double  K_min = 0.1;
static double  Delta_K = 0.01;
static double  K = 0.1;          


void NonlinearMap(double *x, double *y){
    /* Standard Map */
    *y += K * sin(*x);
    *x += *y;

    /* Angle x is module 2Pi */
    *x = fmod(*x, pi2);
    if (*x < 0.0) *x += pi2;
};


/* Callback function: 
   What to do in absence of use input */
void  idle(void){
    /* Increase the stochastic parameter */
    K += Delta_K;
    if(K > K_max) K = K_min;

    /* Redraw the display */
    glutPostRedisplay();
};


/* Initialization for the graphics window */
void winInit(void){
    gluOrtho2D(0.0, pi2, 0.0, pi2);
};

/* Callback function:
    What to do when the display needs redrawing */
void display(void){
    const int    NumberSteps = 1000;
    const int    NumberOrbits = 50;
    const double Delta_x = pi2/(NumberOrbits-1);
    int step, orbit;

    glColor3f(0.0, 0.0, 0.0);
    glClear(GL_COLOR_BUFFER_BIT);
    glColor3f(1.0, 1.0, 1.0);
                
    for (orbit = 0; orbit < NumberOrbits; orbit++){
        double x, y;
        y = 3.1415;
        x = Delta_x * orbit;

        glBegin(GL_POINTS);
        for (step = 0; step < NumberSteps; step++){
          NonlinearMap(&x, &y);
          glVertex2f(x, y);
        };
        glEnd();
     };

     for (orbit = 0; orbit < NumberOrbits; orbit++){
        double x, y;
        x = 3.1415;
        y = Delta_x * orbit;

        glBegin(GL_POINTS);
        for (step = 0; step < NumberSteps; step++){
          NonlinearMap(&x, &y);
          glVertex2f(x, y);
        };
        glEnd();
     };

     glutSwapBuffers();
};


int main(int argc, char **argv)  {  
  /* GLUT Initializations */
  glutInit(&argc, argv);  
  glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA);  
  glutInitWindowPosition(5,5);  
  glutInitWindowSize(300,300);
  
  /* Open Window */
  glutCreateWindow("Order to Chaos");  
  
  /* Window initializations */
  winInit();

  /* Register callback functions */
  glutDisplayFunc(display);  
  glutIdleFunc(idle);

  /* Launch event processing */
  glutMainLoop();  
  
  return 0;  
}  
  
    
    

Dikkate de�er di�er bir farkl�l�k ise display() fonksiyonunun sonunda glutSwapBuffers() fonksiyonunun kullan�lmas�d�r. Pencere ikili arabellek kipinde a��lm��t�r, dolay�s�yla t�m g�r�nt�le�tirme y�nergeleri gizliarabelle�e uygulan�r; bu durumda kullan�c� �eklin �izimini g�rememektedir. �eklin �izimi tamamen bittikten sonra glutSwapBuffers() ile gizli ve g�r�n�r arabelleklerin g�revleri de�i�tirilir Bu teknik olmaks�z�n animasyon d�zg�n bir �ekilde �al��maz.  

Canland�r�m (animasyon) s�resince g�r�nt�lenen baz� �ekiller:

�NEML�: display() geri�a��rma fonksiyonu , idle() fonksiyonundan �nce en az bir kere ya�amage�irilir. Canland�r�mlar�n�z� (animasyonlar�n�z�) yazarken ve display() ile idle() fonksiyonlar�na hangi de�erlerin ge�ti�ine karar verirken bunu akl�n�zdan ��karmay�n.

Do�rular�n ve �okgenlerin �izimi

�nceden s�zedildi�i �uzere glBegin(GLenum mode) �e�itli kipler (modlar) k��e dizilerini alabilir. Ardarda belirtimi yap�lan v₀, v₁,v₂,v₃, v₄,..., v_n-1 uygun bi�imde yorumlanabilir. Olas� kip (mod) de�erleri ve ger�ekle�tirilen eylemler a�a��da belirtilmi�tir:

• GL_POINTS    n k��enin her birisine bir nokta �izer.. 
• GL_LINES    Ba�lant�s�z do�ru dizisi �izer. Do�ru par�alar� v₀ ve v₁, v₂ ve v₃,...vb aras�nda �izdirilirler. n tek ise _n-1 i�leme al�nmaz.. 
• GL_POLYGON    v₀, v₁,..,v _n-1 noktalar�n� k��e alarak bir �okgen �izer.  n en az 3 olmal�d�r, aksi halde hi�bir �ey �izdirilmez. Ayn� zamanda (donan�m�n algorithma k�s�tlamalar�ndan dolay�) bir �okgen kendini kesmemeli ve di�b�key olmal�d�r. 
• GL_TRIANGLES    �nce v₀, v₁ ve v₂; ard�ndan v₃, v₄ ve v₅ vb. noktalar�n� kullanarak bir ��gen dizisi olu�turur. E�er n 3'�n tam kat� de�ilse geri kalan noktalar g�zard� edilir. 
• GL_LINE_STRIP    �nce v₀'dan v₁'e, ard�ndan v₁'den v₂'ye ... do�rular �izer. Son olarak v_n-2'den v_n-1'e bir do�ru �izerek n-1 tane do�ru k�mesi olu�turur. Do�rular� tan�mlayan noktalar �zerinde herhangi bir k�s�t yoktur, do�rular keyfi olarak birbirlerini kesebilirler. 
• GL_LINE_LOOP    v_n-1'den v₀'a do�ru �izerek d�ng�y� kapamasi d���nda GL_LINE_STRIP ile ayn�d�r. 
• GL_QUADS    �nce v₀, v₁, v₂, v₃ noktalar�ndan, sonra v₄, v₅, v₆, v₇ noktalar�ndan ... ge�en d�rtgenler �izer. 
• GL_QUAD_STRIP    �nce v₀, v₁, v₃, v₂ noktalar�ndan, daha sonra v₂, v₃, v₅, v₄ noktalar�ndan ge�en d�rtgenler �izer. 
• GL_TRIANGLE_STRIP    K��e koordinatlar� v₀, v₁, v₂; v₂, v₁, v₃; v₂, v₃, v₄,.. olan ��gen dizisi �izer. S�ralama ��genlerin do�ru y�nlenimli olma g�vencesini sa�layacak bi�imde olup ku�ak bir y�zey par�as� olu�turmak i�in kullan�labilir. 
• GL_TRIANGLE_FAN   ��genlerin �nce v₀, v₁, v₂ ard�ndan v₀,v₂, v₃, v₀, v₃, v₄,... noktalar�ndan �izdirilmesi d���nda GL_TRIANGLE_STRIP ile benzer �al���r. T�m ��genlerin v₀ k��esi ortakt�r. 

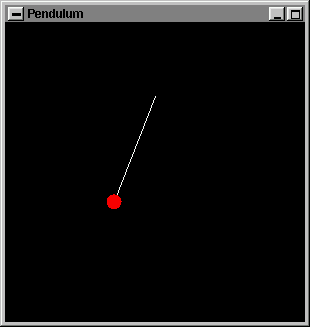
���nc� �rne�imizde GL_LINES ve GL_POLYGON'nun kullan�m�n� g�steren ba�ka bir canland�r�m (animasyon) vard�r. Program� derleyin, kaynak d�zg�s�ne (koduna) bak�n ve nas�l �al��t���n� inceleyin. Example2.c'ye olduk�a benzerdir, burada �ok basit bir sarkac�n devinimi (hareketi) �izdirilmi�tir. Canland�r�m �lk�sel (ideal) bir sarkac�n devinimini �yk�nmektedir (sim�le etmektedir). ��te canland�r�mdan bir anl�kg�r�nt� (snapshot):

�nceden oldu�u gibi yine idle() adl�, amac� saati �al���r tutmak olan yani time de�i�kenini g�ncelleyen, bir geri�a��rma fonksiyonu bulunmaktad�r. display() , iki nesne �izer; sarkac�n ipi ve a��rl��� (s�ras�yla beyaz ve k�rm�z� renklerde). Sarka� koordinatlar�nin devinimi xcenter ve ycenter i�in verilen ba��nt�lardan kapal� olarak elde edilebilmektedir:: 

    

void display(void){
  static double radius = 0.05;
  const double delta_theta = pi2/20;
  double xcenter , ycenter;  
  double x, y;
  double theta = 0.0;

  double current_angle = cos(omega * time);

  glColor3f(0.0, 0.0, 0.0);
  glClear(GL_COLOR_BUFFER_BIT);
  glColor3f(1.0, 1.0, 1.0);

  /* Draw pendulum cord */  
  glColor3f(1.0, 1.0, 1.0);
  glBegin(GL_LINES);
  glVertex2f(0.0, 0.0);
  xcenter = -cord_length * sin(current_angle);
  ycenter = -cord_length * cos(current_angle);
  glVertex2f(xcenter, ycenter);
  glEnd();

  /* Draw pendulum dish */
  glColor3f(1.0, 0.0, 0.0);
  glBegin(GL_POLYGON);
  while (theta <= pi2) {
    x = xcenter + radius * sin(theta);
    y = ycenter + radius * cos(theta);
    glVertex2f(x, y);
    theta += delta_theta;
  };
  glEnd();
  
  glutSwapBuffers();
};

    
    

Al��t�rmalar

��rendiklerinizi uygulamak i�in baz� �neriler:

• In ../../common/January1998/../../common/January1998/example1.c 'deki di�er grafikleri deneyin. Kitapl�ktan, Karga�a (Chaos) ve Fraktallar (Fractals) hakk�nda herhangi bir kitap al�n, i�erisinde pek �ok �rnek bulaca��n�za eminim. �izdirmeden �nce, parametreleri, sistem koordinatlar�n� de�i�tirin ve ard���k grafiklere bunlar� uygulay�n. Bunu e�lenceli bulacaks�n�z. 
• In ../../common/January1998/../../common/January1998/example2.c 'de noktalar�n her birisine renkler ekleyebilirsiniz. �rne�in, �ok ilgin� bir renk d�zg�lemesi (kodlama) olarak, her noktaya y�r�ngenin yerel kararl�l���n� betimleyecek ayr� bir renk verebilirsiniz.  (Physics Review Letters Vol 63, (1989) 1226), �yle ki, devinimyolu karga�asal bir b�lgeye girdi�inde renk k�rm�z�la��r. �rne�in kararl� adasal y�relerde renk mavile�tirilebilir. E�er d�zg�n�z (kodunuz) bu etkiye sahip olursa, �rnekteki fractal'�n �ekli �a��rt�c� olacakt�r. T�revsel denklemler dersini almam�� olanlar i�in biraz ileri olmakla beraber bilgisayarl� grafikte d�n���mlerin ve fractallar�n �st�nl�klerinden yararlanmak i�in bu konuda bilgi edinmeye de�ece�ini vurgulamak gerekmektedir. 
• In �rnek3.c 'deki tekeri (diski) �izdirmekte kullan�lan do�rular�n t�r�n� de�i�tirmeyi deneyin. GL_LINES, GL_TRIANGLES.. gibi fonksiyonlar� kullan�n. Sonu�lar�n� g�zlemleyin. Tekerin (diskin) �izimini eniyilemeye (optimize etmeye) �al���n, her �er�eve i�inde ayn� tekeri (diski) �izmek i�in bir�ok kez sinus ve cosinus hesaplaman�za gerek yoktur. Onlar� bir dizi i�erisine saklayabilirsiniz. �okgen �izimini kullanarak sarkac�n ucuna kutular, elmaslar ya da ne isterseniz onu eklemeye �al���n. Her �er�eve i�ine iki sarka� yaz�n, onlar� ba��ms�z devindirin (hareket ettirin) ya da birbirleriyle �arp��t�r�n. 

Gelecek Yaz�

�u anda s�yleyeceklerim bu kadar. �okgenler hakk�nda daha tart���lacak �ok �ey var. Bir sonraki say�da (Mart 1998) �okgenleri ara�t�rmaya devam edece�iz ve zaten kullanmaya al���k oldu�unuz baz� g�d�mlerin ayr�nt�lar�na inip modellemesini yapaca��z..